内容概览

• 前言
• 时间复杂度
• 空间复杂度
• 总结

 
 

前言

 

作为一名合格的程序员，我们必须要懂得如何写出高质量的代码。然而，代码的核心其实就是算法和数据结构。在将核心能力提升到一个水平之后，我们就比较容易理解和掌握代码重构、设计模式等看似更高级的内容。

而且，知名的互联网企业（微软、谷歌、阿里、腾讯等）在招人的时候必考的项目就是算法与数据结构。所以，想要在软件开发的路上狂奔，您首先就要提高自己的算法和数据结构基础能力。

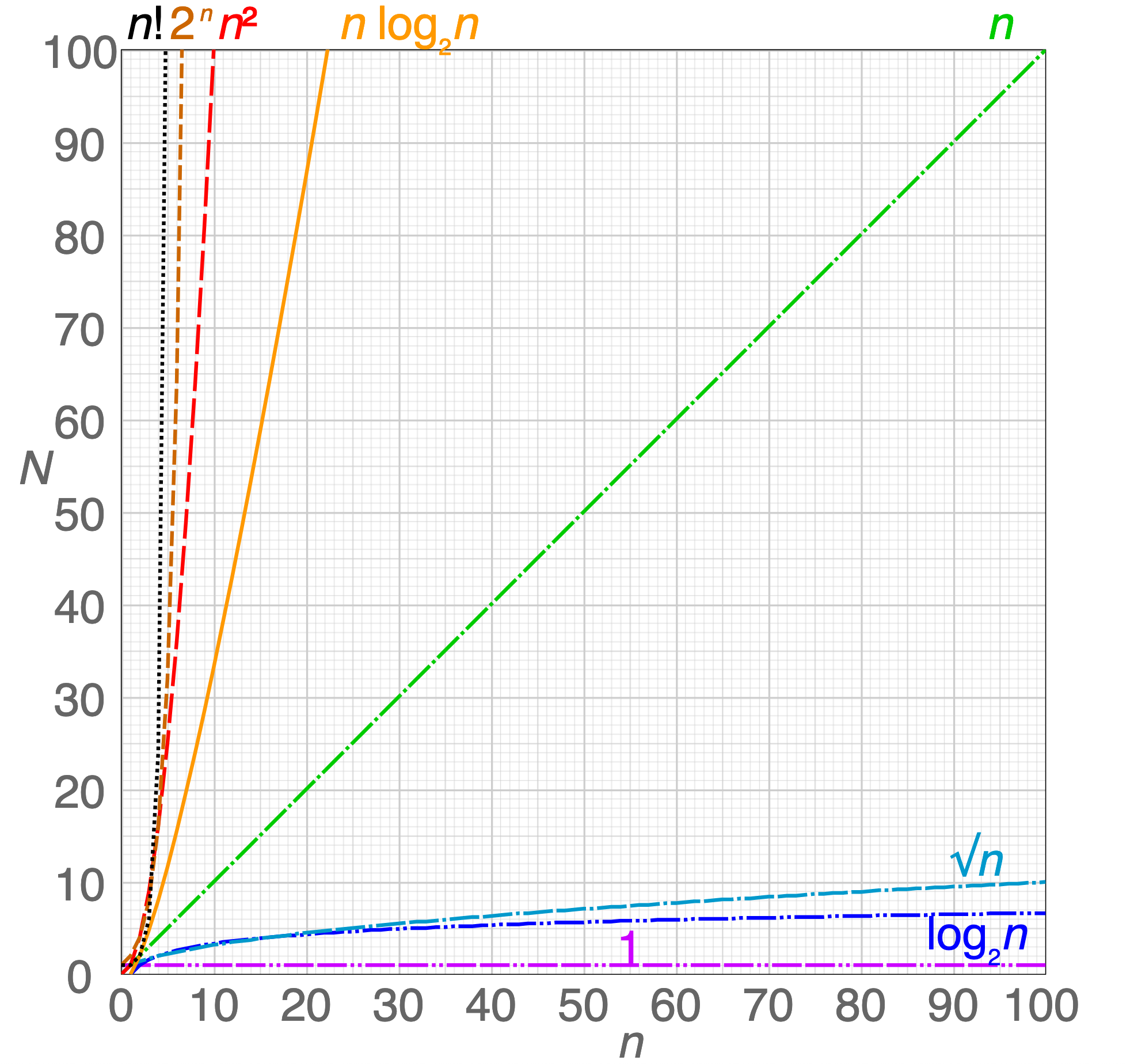
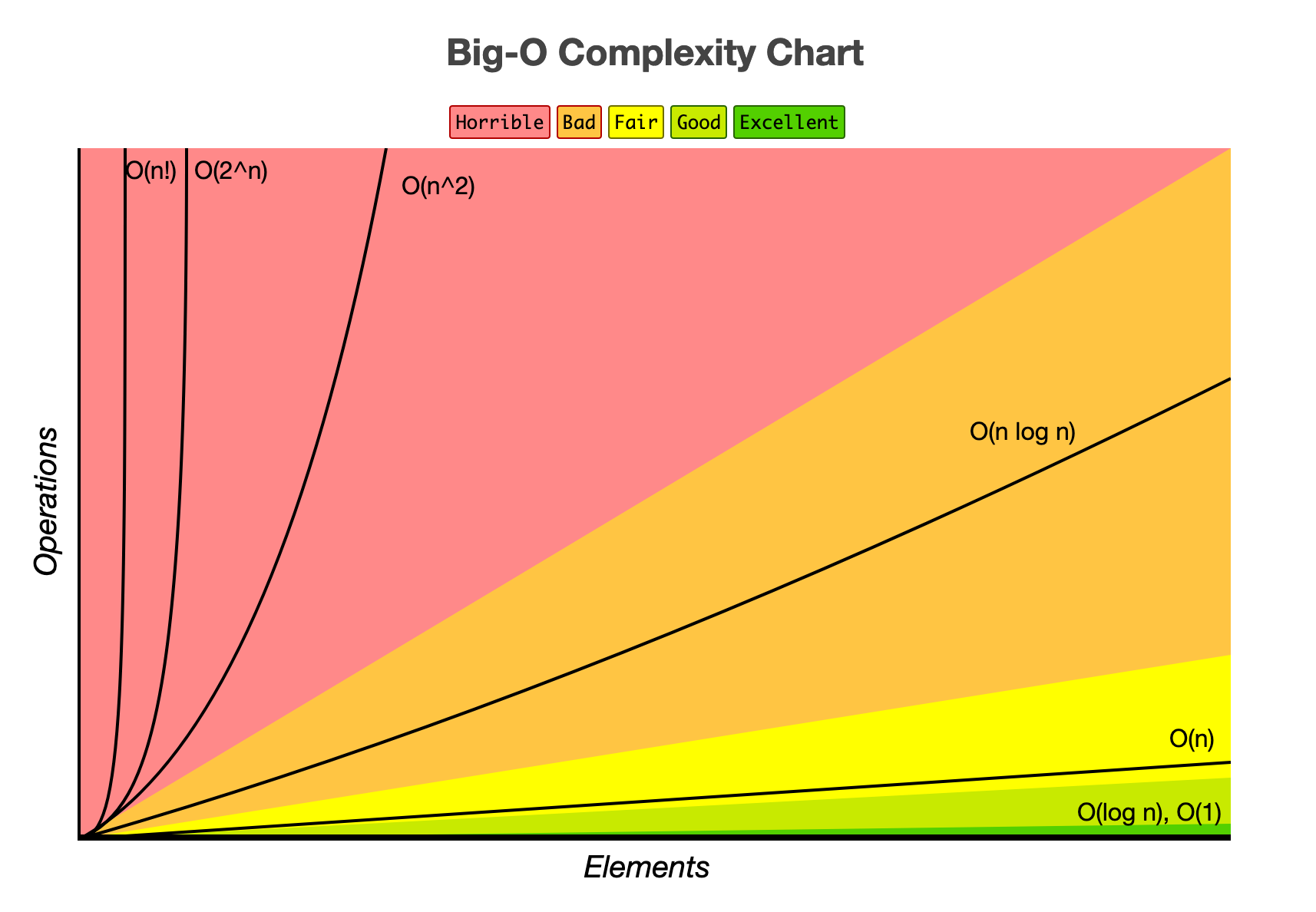
高效的算法和数据结构决定了程序的效率，下图展示了 运算次数 N 和 数据规模 n 之间的关系：

如果现在有1万条数据，此时上图中的 n 就是 10000 。您可以想象一下，n级别的运算次数和 n² 级别的运算次数之间有多大的差别。时间是无价的，我们必须写出高效的程序来完成任务！

我强烈建议您学习覃超老师在 极客时间 上开设的 算法训练营体验课，我已经亲身学习过并推荐给了朋友、同事们。

该课程的内容主要是以视频为主，质量非常高，而且短小精悍。主要涉及：

• 复杂度分析
• 数组、链表、跳表
• 树、二叉树、二叉搜索树
• 递归（代码模板非常给力）

截止 Ficow 创作此文当日，该课程售价还是 9.9 元，性价比还是挺高的。极客时间的新用户还可以免费领取，有效期是一周。赶快行动吧~

因为本文属于 Ficow 陪你学 系列文章，所以 Ficow 也会记录自己的学习历程，并和您分享我自己的学习笔记。欢迎您留言和我交流，大家共同进步！

 
 

时间复杂度

 

时间复杂度：一个算法在运行过程中的执行次数。

 

常见的时间复杂度函数：

O(1)、O(n)、O(nlogn) 、O(n²)、、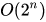

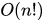
其中，O 是一个记号。计算时间复杂度，只看最高复杂度的运算。时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。
常数级别的复杂度，无论O(1)、O(2)、O(5)，复杂度都是 O(1)。线性级别的复杂度，无论O(n)、O(2n)、O(5n)，复杂度都是 O(n)。然后，以此类推。

 

下面是一些用 Swift 语言编写的示例代码：

• O(1) 时间复杂度：

  let n = 1000
  print(n)
  

• O(n) 时间复杂度（一层循环）：

  let n = 100
  for i in 0..<n {
    print(i)
  }
  for j in 0..<n {
    print(j)
  }
  

• O(nlogn) 时间复杂度：

  var n = 10000, i = 1
  while i < n {
    print(i)
    i *= 2
  }
  

• O(n²) 时间复杂度（两层循环嵌套）：

  for i in 0..<100 {
    for j in 0..<1000 {
        print(i*j)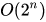
    }
  }
  

• 时间复杂度：

  func fib(_ n: Int) -> Int {
    if n < 2 { return n }
    return fib(n - 1) + fib(n - 2)
  }
  fib(50)
  

 

如果我们要实现累加求和，最生动的比较示例：

• 暴力求解，循环累加，O(n) 时间复杂度：

  let n = 10000
  var sum = 0
  for i in 0..<n {
    sum += i
  }
  print(sum)
  

• 采用数学公式进行计算，O(1) 时间复杂度：

  let n = 10000
  let sum = n * (n + 1) / 2
  print(sum)
  

看官，您感觉如何？性能差距非常大呢~

 

然后，覃超老师还顺便分享了他的面试心得（四件套）：

• 和面试官确认题目的意思，保证理解无误（很多人由于思维模式或者情绪问题，无法准确地理解他人的实际需求）；
• 想出所有可能的解法，并比较它们的时间、空间复杂度（不要急着提交，三思而后行）；
• 找出运行时间最短、内存占用最少的最优解法；
• 写代码并测试结果；

 

如何计算递归的时间复杂度？

例如，求 斐波拉契数列 的第 n 项：F(n) = F(n - 1) + F(n - 2)

如果通过肉眼观察无法计算出该公式的时间复杂度，我们可以 画出递归树 来分析递归调用的时间复杂度。选一个比较容易操作的数，比如 Fib(6) 。

简单画出这个结构后，就可以看到调用的规律（节点数翻倍）：

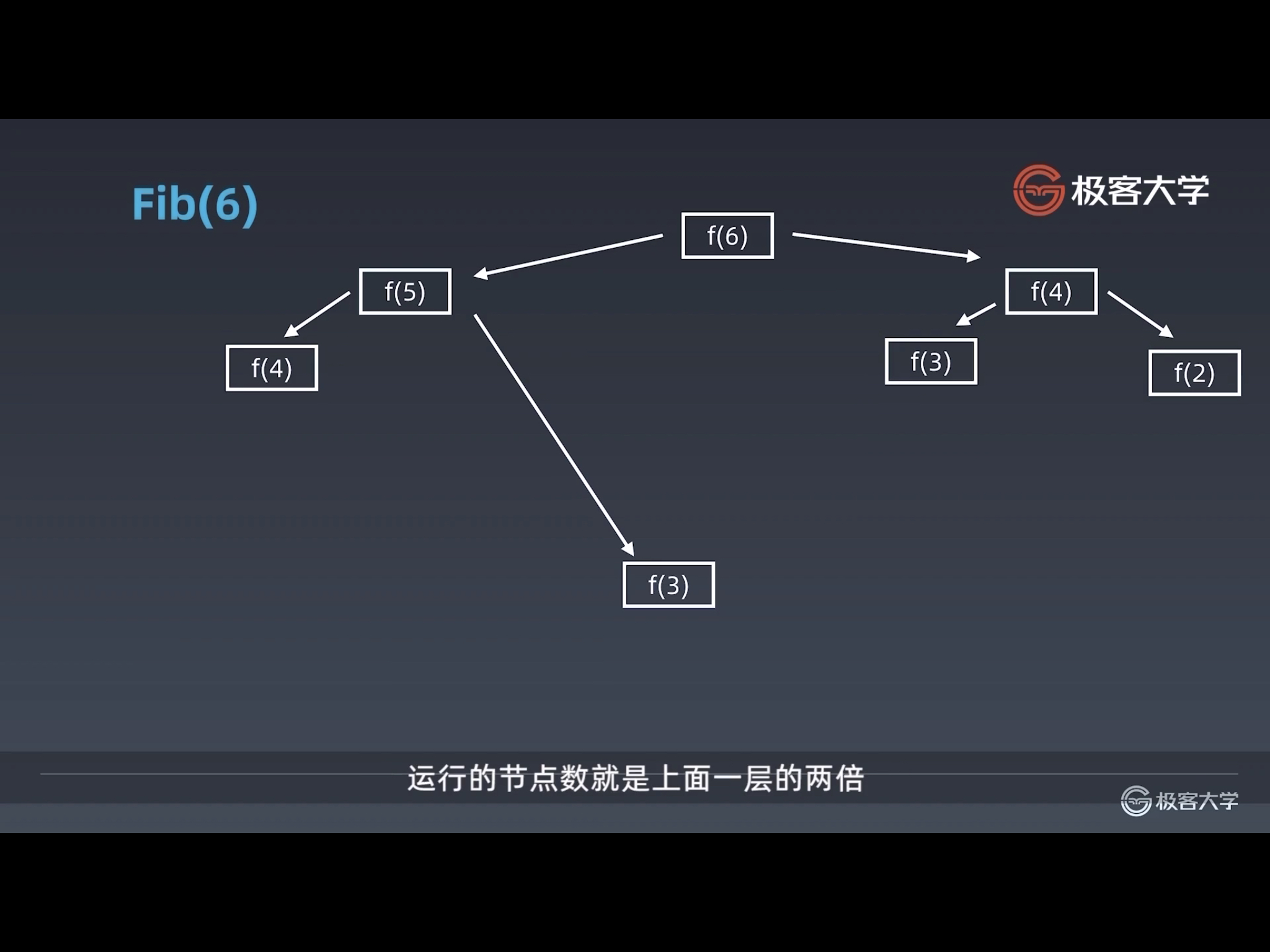
当我们把递归树全部画出来时，就会发现很多被重复计算的节点（可优化）：

这时候，我们可以得出该公式的时间复杂度：O(n²)。

然后，优化被重复计算的节点。解决方案有 2 种：

• 缓存计算结果；
• 将递归调用改为循环；

 

画递归树比较低效，可以使用 主定理 来计算任何递归调用的时间复杂度。

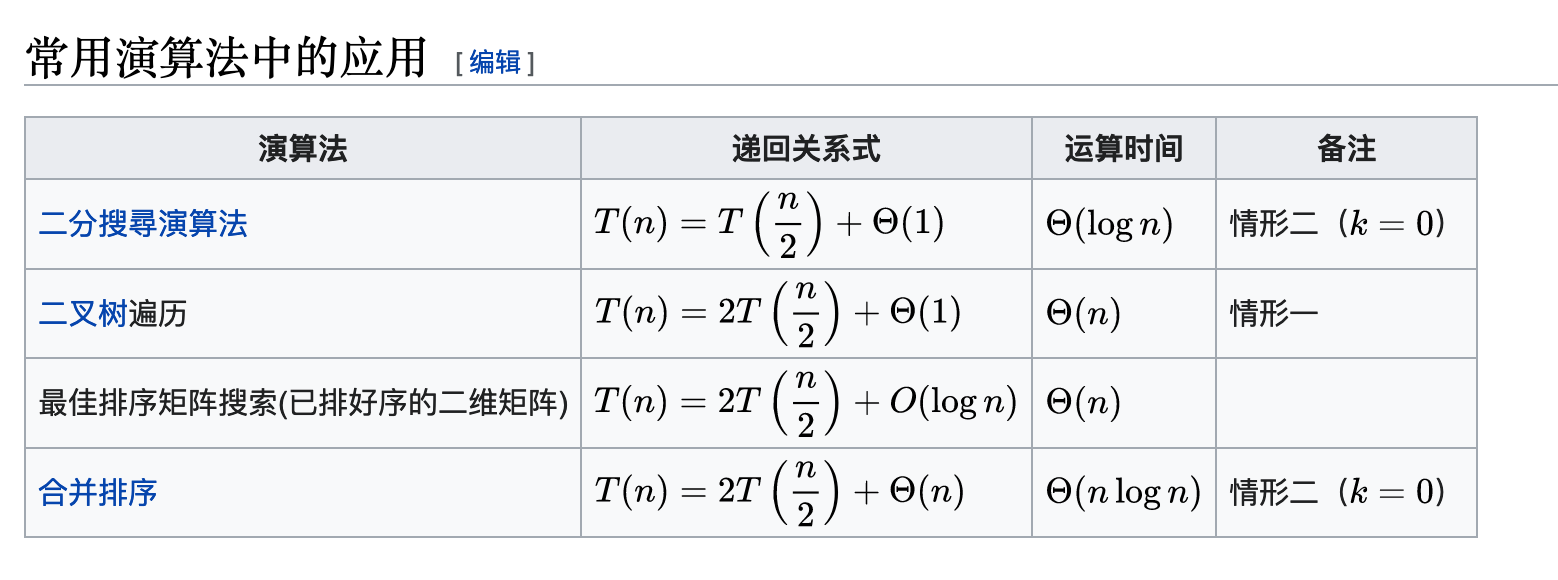
主定理的常用情形主要就是上面的 4 种，理解和记住这几种即可。

下面的这几个思考题比较简单，如果读者知道答案，说明基础还不错。如果读者不知道答案，可以去学习一下覃超老师的视频课：

 
 

空间复杂度

 

空间复杂度：一个算法在运行过程中临时占用存储空间大小的量度。

 

空间复杂度和时间复杂度类似，个人觉得更容易理解：

 

计算原则：

• 如果用了数组，数组所占用的内存空间就是其空间复杂度。比如：一维数组就是 O(n)，行和列一样多的二维数组就是 O(n^2)。
• 如果用了递归，递归需要用到函数调用栈，递归调用的最大深度就是调用栈的最大深度，栈所占用的内存空间就是其空间复杂度。
• 如果又用了数组，又用了递归，两者中空间复杂度最大的就是最终的空间复杂度。

原教学视频中讲解了 LeetCode 上的 爬楼梯 问题，读者感兴趣可以去查看原教学视频。

 

覃超老师的 刻意练习 秘诀：

• 常用工具配置
• 基本功和编程指法
• 常见的时间、空间复杂度

到搜索引擎去搜索 Best Practices 或者 Top Tips，找到相关的优质内容。比如，Ficow 就在 Github 找到了一份比较优质的iOS开发资料 ios-good-practices 以及Android开发资料 android-best-practices。

 
 

总结

 

学习编程，必须要理解和练习才能真正掌握所学的内容。推荐您去 LeetCode，然后针对性地学习和练习您需要掌握的内容。

 

复杂度分析的要点：

• 只看最高复杂度的运算；
• 常见的复杂度函数： O(1)、O(n)、O(nlogn) 、O(n²)、、
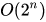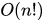
• 记住 运算次数 N 和 数据规模 n 之间的关系，脑海中要有这样一张图：

推荐继续阅读：2. 数组、链表、跳表 —— Ficow 陪你学算法和数据结构

 

参考内容：

极客时间
算法训练营体验课
LeetCode
LeetCode - 中文站
主定理
主定理 - 维基百科
如何理解算法时间复杂度的表示法，例如 O(n²)、O(n)、O(1)、O(nlogn) 等？