内容概览

• 前言
• 树（Tree）
• 二叉树（Binary Tree）
• 二叉搜索树（Binary Search Tree）
• 实战题目
• 总结

 

前言

 

在 2. 数组、链表、跳表 —— Ficow 陪你学算法和数据结构 中，Ficow 和您分享了自己的学习笔记。之前学习的链表是一种常见的一维数据结构，但是它的查询时间复杂度较高，所以科学家发明了跳表来解决这个问题。

在利用跳表进行加速的过程中，核心的思想就是 升维。接下来，让我们开始学习常见的二维数据结构：树 和 图。

 

在开始阅读后文之前，我强烈建议您学习覃超老师在 极客时间 上开设的 算法训练营体验课，我已经亲身学习过并推荐给了朋友、同事们。

该课程的内容主要是以视频为主，质量非常高，而且短小精悍。主要涉及：

• 复杂度分析
• 数组、链表、跳表
• 树、二叉树、二叉搜索树
• 递归（代码模板非常给力）

截止 Ficow 创作此文当日，该课程售价还是 9.9 元，性价比还是挺高的。极客时间的新用户还可以免费领取，有效期是一周。赶快行动吧~

因为本文属于 Ficow 陪你入门 系列文章，所以 Ficow 也会记录自己的学习历程，并和您分享我自己的 学习笔记。欢迎您留言和我交流，大家共同进步！

 

树（Tree）

 

如果链表的结点拥有多个 next 指针，这时候的链表就变成了一棵树！

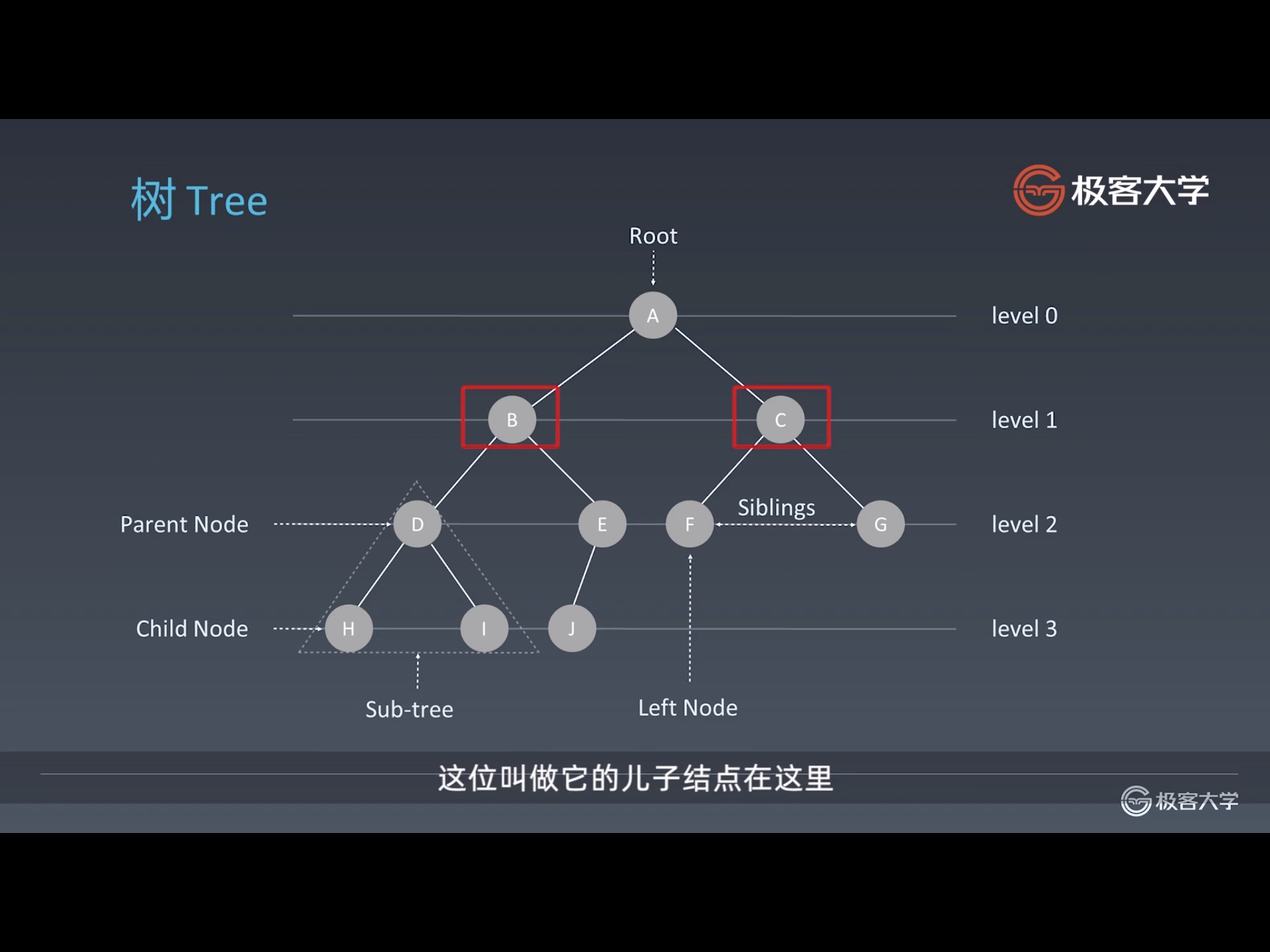
上图中，A 结点为树的根结点，B、C结点分别为 A 结点的左子结点 和右子结点。同时，树还分了层，比如图中的 level 0, level 1, …

 

二叉树（Binary Tree）

 

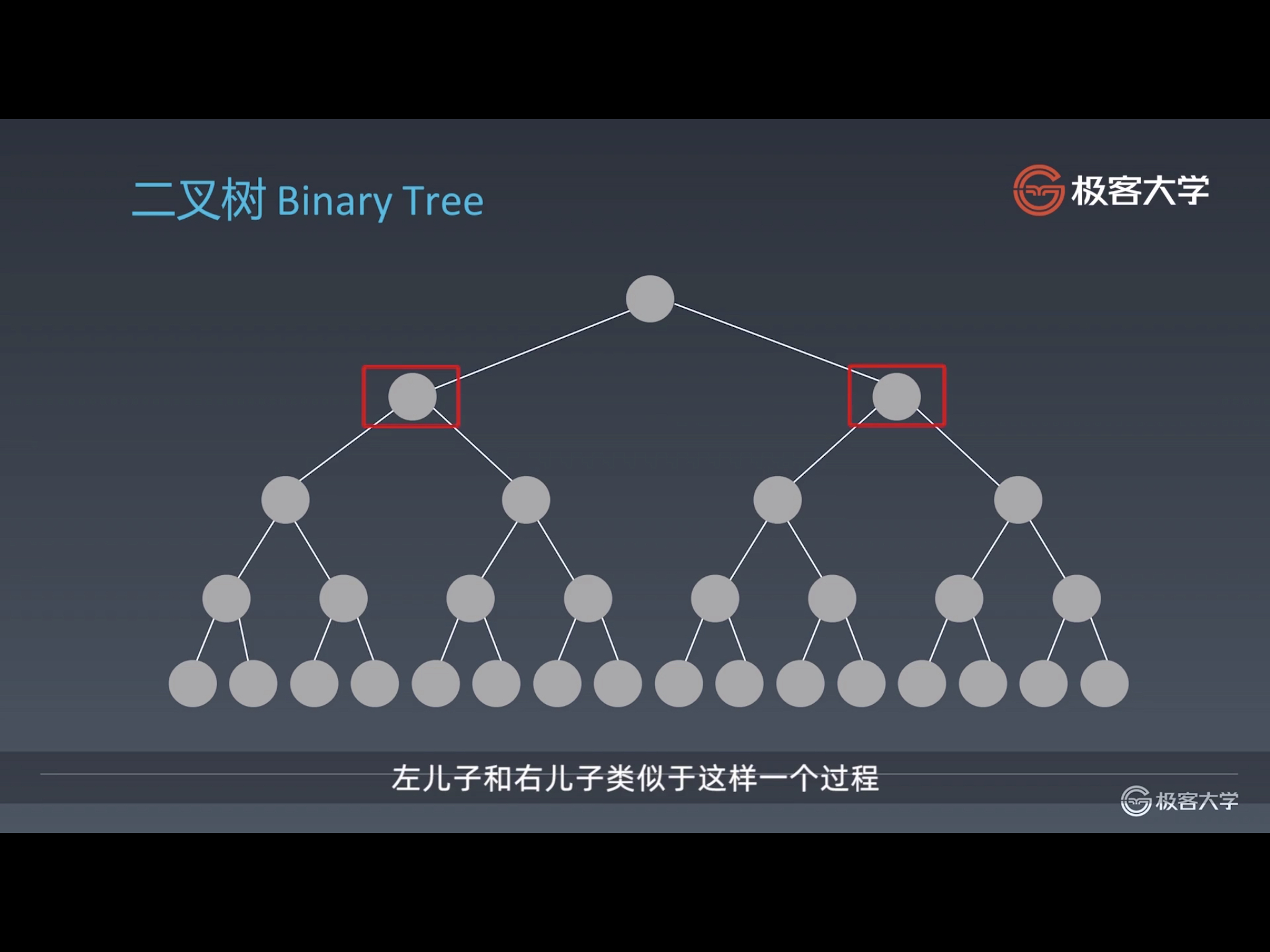
二叉树是最常见的树，每个结点最多拥有两个子结点。

树和图最关键的差别在于是否存在环。如果不存在环，就是树；如果存在环，就是图。

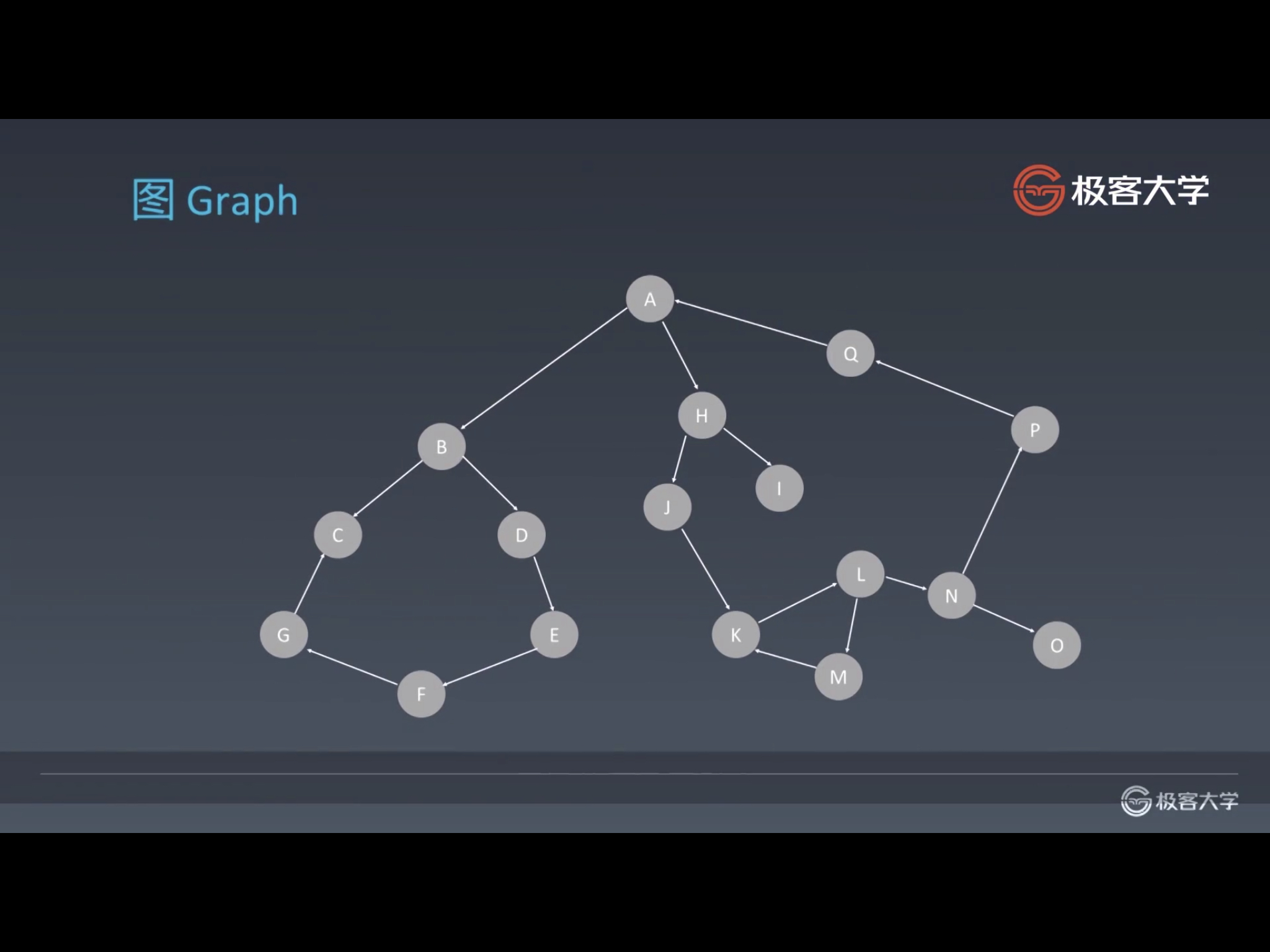
可以这样理解：链表就是特殊化(每个结点最多只有一个子结点)的树，树就是特殊化(不存在环)的图。

 

常见的树的定义：

树的常见场景：

• 当我们调用递归函数时，递归调用的状态就是呈树状的。
• 当人工智能在分析下棋时，每一步落子之后，余下的状态就都可以进行推测，而这个用于推测的数据结构就是一个决策树。
• 人在生活中的一次次决策的不同，就会导致最终生活状况的不同，这所有可能的生活状况就是一个状态树。

二叉树的遍历：

主要分为：前序、中序、后序：

基于 Python 的示例代码(递归调用，非常简短)：

根据树的定义，其没办法进行有效的循环，所以常见的树的遍历方式为递归。
非要进行循环遍历，可以采用 BFS(广度优先遍历)算法 来强制进行遍历，但是写法比递归调用更复杂。

 

二叉搜索树（Binary Search Tree）

 

在普通的树（结点中的值是无序的）中查找特定的值，就需要遍历所有的结点，时间复杂度为 O(n)。通常我们会把树中的值按照某种顺序来进行组织，在查找的时候就会更加高效。

请注意上图中黄色高亮部分的内容！ 所有结点 ！！！在比较的时候，要比较左子树中所有的结点，而不是单个左子结点！！！

实际的二叉搜索树示例：

 

二叉搜索树常见操作：

• 查询
• 插入新结点
• 删除（删除非叶子结点时，把大于被删除结点的结点移动到被删除结点的位置）

Demo：https://visualgo.net/zh/bst

以上操作的时间复杂度都为：O(logn)。

不过，有一种特殊情况，树会退化为一个链表。此时，查询操作的时间复杂度由 O(logn) 变为 O(n)：

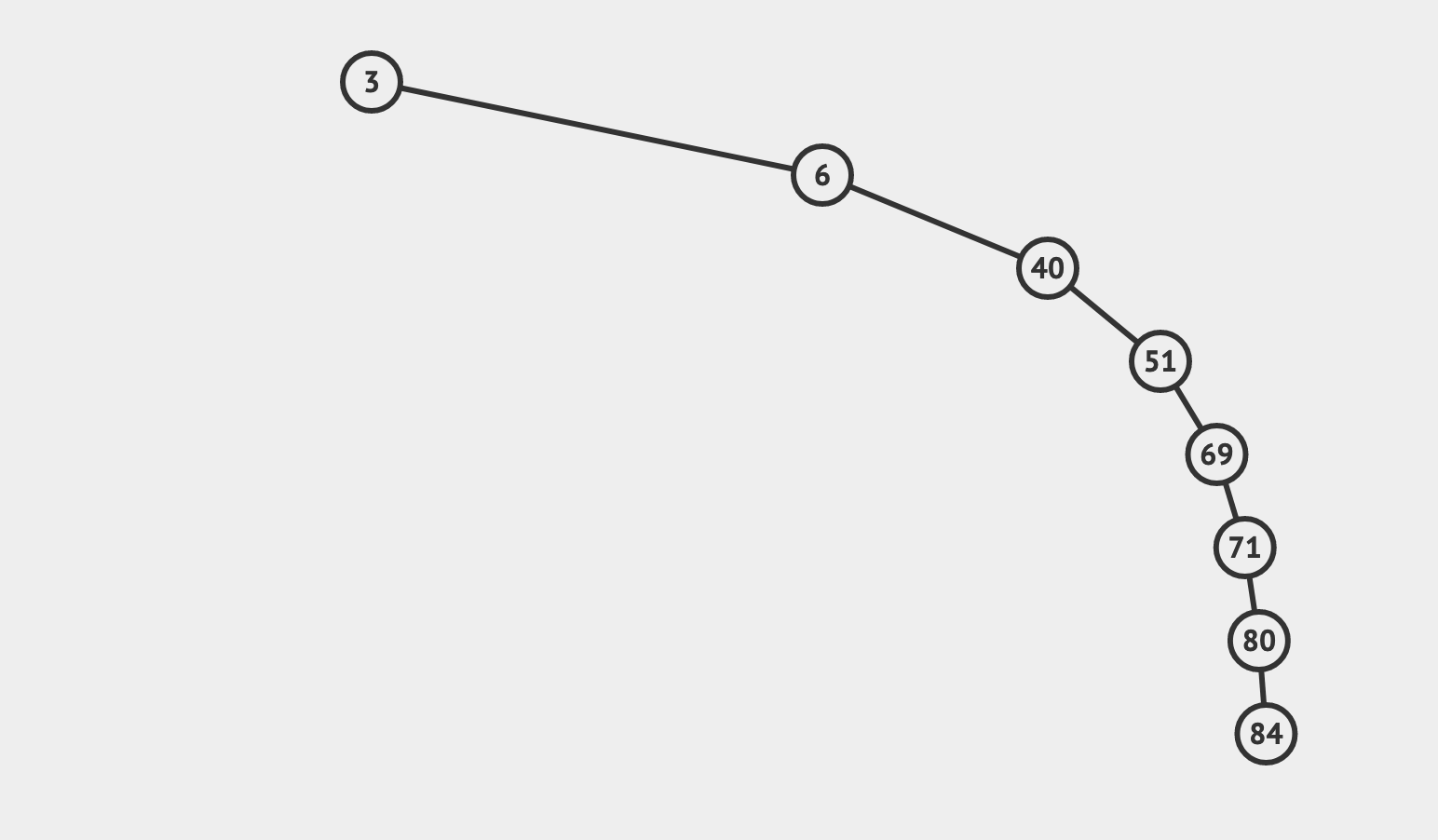
如何解决这个问题呢？可以考虑使用 平衡二叉树。

 

实战题目

 

二叉树的中序、先序、后序遍历：
https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

N叉树的先序遍历：
https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/

N叉树的层遍历（需要用到BFS广度优先搜索算法）：
https://leetcode-cn.com/problems/n-ary-tree-level-order-traversal/

 

练题的操作步骤：

• 写出自己的思路，多种解法 都写下来，最后再去比较并找出最好的解法；
• 用代码实现自己的解法，然后用题目提供的测试数据进行测试（多尝试几组数据，比如特殊情况）；
• 测试通过后即可提交代码，然后查看该代码的审题结果，主要看耗时和时间复杂度；
• 寻求反馈：Code Review（尽量这样做）、查看题解（不要在糟糕的解法上浪费时间），理解优秀解法的思路还有代码的写法，然后自己参照着实践几遍；
• 复制题解的网址，删除域名中的 -cn，然后打开 LeetCode 国际站，在 题目的 Discuss 页面选择 Most Votes，消化吸收各种优秀的解法，同时提升英语水平。
• 把这个题目刷 5遍，5遍，5遍！！！千万不要只刷一遍！！！

 

总结

 

有同事或者朋友说过，这些东西平时根本没有用到过，学了有什么用？

然而，这只是自己目前的工作没有用到而已，哪里可以保证以后的工作里面用不到呢？除非，我们一辈子都重复做一样的工作，不然就有可能在某一天需要用到这些东西。比如：去更优秀的公司工作，我们就经常需要造轮子，而这个时候就需要用到这些知识。

再者，学习这些数据结构可以学习其设计思路，再遇到类似的问题时就可以参考这种思路来高效地解决自己遇到的问题。更何况，在练习这些数据结构时，自己的编程技能也可以得到提升。有时候，我们就是容易忽略这些看不到的好处。

不管怎样，如果您热爱编程、热爱您所做的软件开发工作，那么提升基本功一定是利大于弊的。技多不压身，是不是~

 

推荐继续阅读：4. 递归 —— Ficow 陪你学算法和数据结构

 

参考内容：

极客时间
算法训练营体验课
LeetCode
LeetCode - 中文站