内容概览

• 前言
• 爬楼梯问题
• 递归
• 动态规划
• 矩阵快速幂
  • 矩阵乘法
  • 快速幂算法
• 通项公式
• 打表
• 总结

 

前言

 

如果您有过刷算法题的经历，那么您一定知道，爬楼梯问题 是一个非常经典的算法题目。

如果您不曾有过刷算法题的经历，而且您想提高自己的逻辑思维能力和编码水平，那么 Ficow 建议您花些时间来练习算法题，它确实可以有效地帮助您提升编码的效率和质量。

Ficow 认为这个题目非常棒！原因在于，通过练习掌握这样一个题目，我们就可以学到很多种解法（开拓视野），大致如下：

• 递归
• 动态规划
• 矩阵快速幂
• 通项公式
• 打表

不过，这里面让我觉得比较有意思的还是【矩阵快速幂】解法。由于水平有限（线性代数几乎都忘干净了），相比于理解其他非数学解法，我在理解这个解法时耗费了最多的时间。

言归正传，让我们一起来看看这个经典题目到底有多么棒吧~

 

爬楼梯问题

 

这是 Leetcode 的题目链接，该题目描述如下：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

通过示例可以看出，如果要求出爬 3 层楼梯的方法数，可以先求出爬 1层到达第 3 层(n - 1)和爬 2 层到达第 3 层(n - 2)的方法数，相加之和即为最终结果。

 

递归

 

通过递归，我们很容易实现上述【自顶向下】的解法，Swift 代码如下：

func climbStairsWithRecursion(_ n: Int) -> Int {
    var memo = [Int: Int]() // 注意缓存重复的递归状态
    func f(_ n: Int) -> Int {
        if n < 3 { return n }
        if let v = memo[n] { return v }
        let v = f(n - 1) + f(n - 2)
        memo[n] = v
        return v
    }
    return f(n)
}

复杂度分析如下：

• 时间复杂度：O(n)，函数体内没有循环语句，递归调用时没有重复状态，只是利用递归栈进行简单的加法运算。
• 空间复杂度：O(n)，字典缓存重复递归状态占用的空间。

提交之后的执行效果如下：

可以看到，虽然这个解法通过了所有测试用例，但是执行的效率其实不太高。

那我们再继续尝试其他解法吧~

 

动态规划

 

仔细观察上面的递归解法的代码，您会发现：

let v = f(n - 1) + f(n - 2)

就是整个解法的核心代码，要求得 f(n)，就先要求得 f(n - 1)、f(n - 2)，最终 f(n) 即为二者之和。

那我们是不是也可以不用递归【自顶向下】的方式来求解呢？

可以的，我们可以通过动态规划来【自底向上】地递推求解！这样，就可以省掉很多递归调用占用的函数调用栈。

 

那我们该怎么做呢？

首先，我们需要定义状态和选择，状态为当前的楼层数（1 <= n <= 45），选择为可以跳跃的步数（1, 2）。

然后，根据状态和选择，我们可以定义一个整型的数组 f 作为动态规划数组，f[i] 代表跳跃到 i 层楼有多少种方法。
为了简化最终返回值，我们可以将 f 的长度定义为 n + 1，最终结果即为 f[n]。

最后，上面的 f(n) = f(n - 1) + f(n - 2) 即为状态转移方程。动态规划的状态转移方程是基于数学归纳法构建的，即：当 n=1 时命题成立，假设 n=m 时命题成立，那么可以推导出在 n=m+1 时命题也成立。

当然，我们还要考虑一些极端情况，比如：n 为 1、2 时，可以直接返回结果，不应该利用状态转移方程进行计算。在进行递推前，也需要为 i 为 1、2 时的base case进行赋值，否则后续的递推将得到错误的结果。

 

Swift 代码如下：

func climbStairsWithDP(_ n: Int) -> Int {
    if n < 3 { return n } // edge cases 直接返回
    var f = [Int](repeating: 0, count: n + 1)
    // base cases
    f[1] = 1
    f[2] = 2
    for i in stride(from: 3, through: n, by: 1) {
        f[i] = f[i - 1] + f[i - 2]
    }
    return f[n]
}

复杂度分析如下：

• 时间复杂度：O(n)，函数体内有一个循环语句，从 3 到 n，进行简单的加法运算。
• 空间复杂度：O(n)，动态规划数组占用的空间。

提交之后的执行效果：

嗯，这个动态规划的击败了 100% 的用户，so much better~

 

状态压缩

仔细观察上面的代码，我们会发现每次循环只需要用到 f[i - 1] 和 f[i - 2]，所以我们可以用临时变量来代替 f 数组，Swift 代码如下：

func climbStairsWithCompressedDP(_ n: Int) -> Int {
    var a = 0, b = 0, c = 1
    for _ in 1...n {
        a = b
        b = c
        c = a + b
    }
    return c
}

此时，空间复杂度已经从 O(n) 压缩到了 O(1)。提交之后的执行效果：

看来动态规划解法已经很强了呀，还有更强的解法？有的呢~

坚持住，其实后面的解法也不是很难的呢。世上无难事，只怕有心人，嘿嘿~

 

矩阵快速幂

 

上面的动态规划解法的时间复杂度为 O(n)，如果通过矩阵快速幂来解决这个问题，时间复杂度可以进一步压缩到 O(logn)！

这里是 LeetCode 官方的题解，方法二即为矩阵快速幂。不过，Ficow 认为该题解跳过了很多必要的知识点。

如下图所示，您是否也好奇，这些红色框标记的部分是怎么弄出来的？

---

---

如果您也有相同的疑问，那么，希望 Ficow 的讲解能够帮助到您。

在本节中，Ficow 会将矩阵快速幂这个知识点拆分为两个部分：矩阵运算 和 快速幂算法。

因为，这个解法其实就是将上面的动态规划递推公式变换为矩阵乘法运算（这个变换过程并没有改善时间复杂度），然后再利用快速幂算法来加速矩阵乘法运算（快速幂算法可以将求幂操作的时间复杂度由 O(n) 压缩到 O(logn)）。

 

矩阵运算

关于矩阵运算，《面试必考的「矩阵快速幂」考点汇总》 这篇文章里面讲解了很多相关的 线性代数 概念，如：矩阵加减法、乘法的运算规律，以及矩阵乘法满足分配律、结合律但不满足交换律等内容。东西虽多，但是其实不难理解，只需要您有耐心就可以了。

矩阵乘法

在本节中，我主要想通过示例来详细讲解一些题解中未涉及到的重要内容。以下图中的矩阵乘法运算为例：

左边的矩阵是这样算出来的：

首先，用 -1 2 1 去分别乘以 2 -3 1，即：(-1) x 2 + 2 x (-3) + 1 x 1 = -7；
然后，用 -1 2 1 去分别乘以 -1 -2 3，即：(-1) x (-1) + 2 x (-2) + 1 x 3 = 0；
同理，用 5 3 2 去分别乘以 2 -3 1，即：5 x 2 + 3 x (-3) + 1 x 2 = 3；
最后，用 5 3 2 去分别乘以 -1 -2 3，即：5 x (-1) + 3 x (-2) + 2 x 3 = -5；

其实，挺容易理解的，对吧？我们继续吧~

我相信，这时候您已经可以自行算出上面的截图中的某些矩阵乘法的结果了。

构造矩阵

构造矩阵的部分，我们可以参考 《面试必考的「矩阵快速幂」考点汇总》 一文中的内容：

---

转移矩阵

关于转移矩阵这部分的内容，让我们结合官方题解的内容来进行理解：

举个例子，我们一起来算一算上面这个式子。

先算上面的那一行：1 x f(n) + 1 x f(n - 1) = f(n) + f(n - 1) = f(n + 1)；
然后算下面那一行：1 x f(n) + 0 x f(n - 1) = f(n)；

通过计算这个矩阵乘法，您就可以理解那个转移矩阵是如何得出的。但是，下面这个式子是怎么算出来的呢？

---

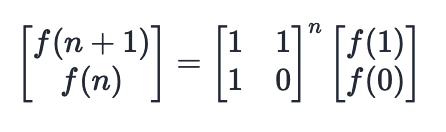
以下是 Ficow 在草稿纸上进行计算的手稿（书写有些潦草），供您参考：

这时候您会发现，变换后的式子的计算量主要集中在求矩阵的幂。

 

快速幂算法

接下来，我们就要通过快速幂算法来加速求解以下矩阵的结果：

这是 LeetCode 官方的讲解内容 Pow(x, n) 快速幂解法，实现的方式有两种：递归和迭代。

递归版本

func fastModWithRecursion(_ x: Double, _ n: Int) -> Double {
    func mod(x: Double, n: Int) -> Double {
        if n == 0 { return 1 }
        let y = mod(x: x, n: n >> 1)
        return n & 1 == 1 ? y * y * x : y * y
    }
    return n >= 0 ? mod(x: x, n: n) : 1/mod(x: x, n: -n)
}

其实，递归实现的思路比较简单。如果是非负数，直接求解；如果是负数，就加上负号之后求解，最后取倒数（即：x -> 1/x）。

在求解的过程中，如果如果 n 为偶数，则直接返回平方后的值，否则需要在平方的基础上再乘以一个底数 x。

迭代版本

func fastModWithIteration(_ x: Double, _ n: Int) -> Double {
    func f(x: Double, n: Int) -> Double {
        var ans = 1 as Double, n = n, xContribute = x
        while n > 0 {
            if n & 1 == 1 { ans *= xContribute }
            xContribute *= xContribute
            n >>= 1
        }
        return ans
    }
    return n >= 0 ? f(x: x, n: n) : 1/f(x: x, n: -n)
}

对于这个解法， 其实就是在不断让 n 除以 2 的过程中，xContribute 不断累乘 x。当 n 的最低二进制位为 1 时，就让最终结果 ans 乘以当前的累乘值 xContribute。

以官方题解中求解 x^77 为例，77 的二进制为 1001101，计算的过程如下：

所以，ans = x ^ 77 = 1 x^1 x^4 x^8 x^64。通过这样的变换，求幂不需要累乘77次，只需要累乘 4 次！

也就是实现了将时间复杂度为 O(n) 的累乘转换成了时间复杂度为 O(logn) 的快速幂。

 

矩阵快速幂

到这里，我们已经具备了理解矩阵快速幂解法的大部分基础知识。接下来，我们开始求解爬楼梯问题，Swift 代码如下所示：

func matrixFastPower(_ n: Int) -> Int {
    // 系数矩阵 q
    var q = [[1, 1], [1, 0]]
    // 让两个矩阵相乘
    func multiply(a: [[Int]], b: [[Int]]) -> [[Int]] {
        var c = [[Int]](repeating: [Int](repeating: 0, count: 2), count: 2)
        for i in 0..<2 {
            for j in 0..<2 {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j] // 矩阵乘法
            }
        }
        return c
    }
    // 快速幂算法的核心代码没有变化
    func pow(n: Int) -> [[Int]] {
        // 单位矩阵 ret
        var ret = [[1, 0], [0, 1]], n = n
        while n > 0 {
            if n & 1 == 1 {
                ret = multiply(a: ret, b: q)
            }
            n >>= 1 // 二进制右移一位，相当于除以 2 取整
            q = multiply(a: q, b: q)
        }
        return ret
    }
    let res = pow(n: n)
    return res[0][0]
}

注意事项：

• 如果您还是没明白这部分的知识，您可以考虑结合 【宫水三叶】小姐姐的题解来理解：泰波那切数 —— 一题四解。我个人认为该文章可以有效地帮助您理解 如何获得以上示例代码中的系数矩阵 q。
• 除此之外，以上示例代码中的 pow 函数内有一个 ret 矩阵，这是一个 单位矩阵。之前的快速幂算法需要用 ans = 1 来累乘运算过程中的幂值，这里的单位矩阵就是扮演 ans = 1 的角色。其实，单位矩阵就是矩阵运算里面的 1。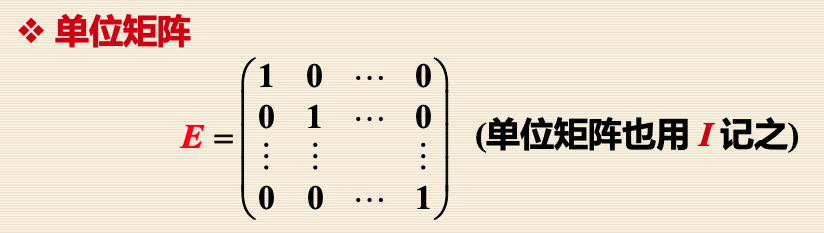
  

如果您结合了 面试必考的「矩阵快速幂」考点汇总 这篇文章中关于 【斐波那契数】 问题的题解来理解本文内容，那么您一定要注意这句话：

为什么爬楼梯问题需要计算快速幂到 n，而求斐波那契问题需要计算到 n - 1 呢？爬楼梯问题和求斐波那契数有一个重要的区别：
求斐波那契数是从0开始的，即：0, 1, 1, 2, 3, 5, 8, 13。而爬楼梯问题是从 1 开始的，即：1, 2, 3, 5, 8, 13。

所以，爬楼梯的快速幂直接算到 n 即可，如果是求斐波那契数问题，就需要计算快速幂到 n - 1。

如果您成功理解了这一节的内容，那么恭喜您，您已经成功掌握了快速幂算法。棒棒哒~

 

通项公式

 

很多时候，这种数列求值的问题都可以用数学知识来攻破（真正的高手往往很擅长降维打击）。
比如，这里可以根据递推方程求出特征方程，然后求解，最终得到一个通项公式。示例代码如下：

func fibonacciFormula(_ n: Int) -> Int {
    let sqrt5 = sqrt(5)
    let divisor = Double(n + 1)
    let fibn: Double = pow((1 + sqrt5) / 2, divisor) - pow((1 - sqrt5) / 2, divisor)
    return Int(round(fibn / sqrt5))
}

这部分的内容比矩阵快速幂还要难很多，Ficow 功力有限，所以更推荐您参考 二阶常系数齐次线性递推数列 来理解。

对于齐次和非齐次的概念，您可以参考以下内容：

 

打表

 

除此之外，因为 n 的大小是限制了的，您还可以考虑一次性算出有效范围内所有的解，然后缓存到静态变量中。

之后，所有的操作就只是读缓存而已，更加高效~

示例代码如下：

class Solution {
    static var values = [Int](repeating: -1, count: 46)

    func climbStairs(_ n: Int) -> Int {
        if Self.values[n] != -1 { return Self.values[n] }
        var a = 0, b = 0, c = 1
        for i in 1...45 {
            a = b
            b = c
            c = a + b
            Self.values[i] = c
        }
        return Self.values[n]
    }
}

 

总结

 

学习算法的路是永无止境的，学贵有恒！虽然，越学越觉得自己很无知，哈哈。

学习是最无聊的，同时也是最有趣的。不管怎样，这都是一段很特别的经历，enjoy the journey~

 

参考内容：
爬楼梯 - LeetCode
Pow(x, n) - LeetCode
刷算法题必备的数学考点汇总
面试必考的「矩阵快速幂」考点汇总
【宫水三叶】一题四解 :「迭代」&「递归」&「矩阵快速幂」&「打表」
Pow(x, n) 快速幂解法 - LeetCode
二阶常系数齐次线性递推数列